플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)은 그래프에서 가능한 모든 노드 쌍에 대해 최단 거리를 구하는 알고리즘이다. DynamicProgramming 기술에 의거한다.
"거쳐가는 정점"을 기준으로 최단거리를 구한다.
코드는 단순히 반복문을 3번 중첩시키기만 하면 되기 때문에 구현에 있어 크게 어려운 부분은 없다.
단, 유의하여야 할 점은 for문에서 가운데 노드(m)이 제일 위에 있어야 한다는 점이다.
시간복잡도는 O(V^3)이다. 다익스트라 알고리즘과는 달리 모든 노드 쌍에 대해 최단 거리를 구하고, 음의 가중치를 가지는 그래프에서도 쓸 수 있다.
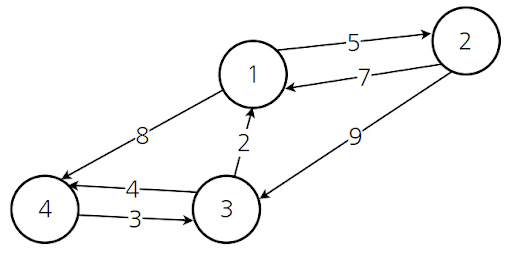
1을 거쳐가는 경우를 갱신한다 하면
=> D[2,3] 과 ( D[2,1] + D[1,3] ) 을 비교하여 최솟값으로 업데이트한다.
=> min( 9, 7+inf) = 9
이러한 방식대로 업데이트하면 된다.
아래는 플로이드 워셜을 구현한 c코드이다.
for(m=1; m<=N; m++)
for(s=1; s<=N; s++)
for(e=1; e<=N; e++)
if (d[s][e] > d[s][m] + d[m][e])
d[s][e] = d[s][m] + d[m][e];
24. 플로이드 와샬(Floyd Warshall) 알고리즘
지난 시간에는 다익스트라(Dijkstra) 알고리즘에 대해 학습했습니다. 다익스트라 알고리즘은 하나의 정점...
blog.naver.com
플로이드-워셜 알고리즘 - 나무위키
이 저작물은 CC BY-NC-SA 2.0 KR에 따라 이용할 수 있습니다. (단, 라이선스가 명시된 일부 문서 및 삽화 제외) 기여하신 문서의 저작권은 각 기여자에게 있으며, 각 기여자는 기여하신 부분의 저작권
namu.wiki
반응형
'코딩테스트 > 알고리즘 개념정리' 카테고리의 다른 글
| 그래프(Graph) 코드 구현 및 이해 (0) | 2021.04.07 |
|---|---|
| 백트래킹(BackTracking, DFS/BFS), N과M(1) (0) | 2021.03.30 |
| 그래프 이론(싸이클, 최소신장트리, 위상 정렬) (0) | 2020.11.25 |
| DFS/BFS 개념정리 (0) | 2020.11.04 |
| DP(=다이나믹 프로그래밍,Dynamic Programming) 심화 (0) | 2020.10.13 |