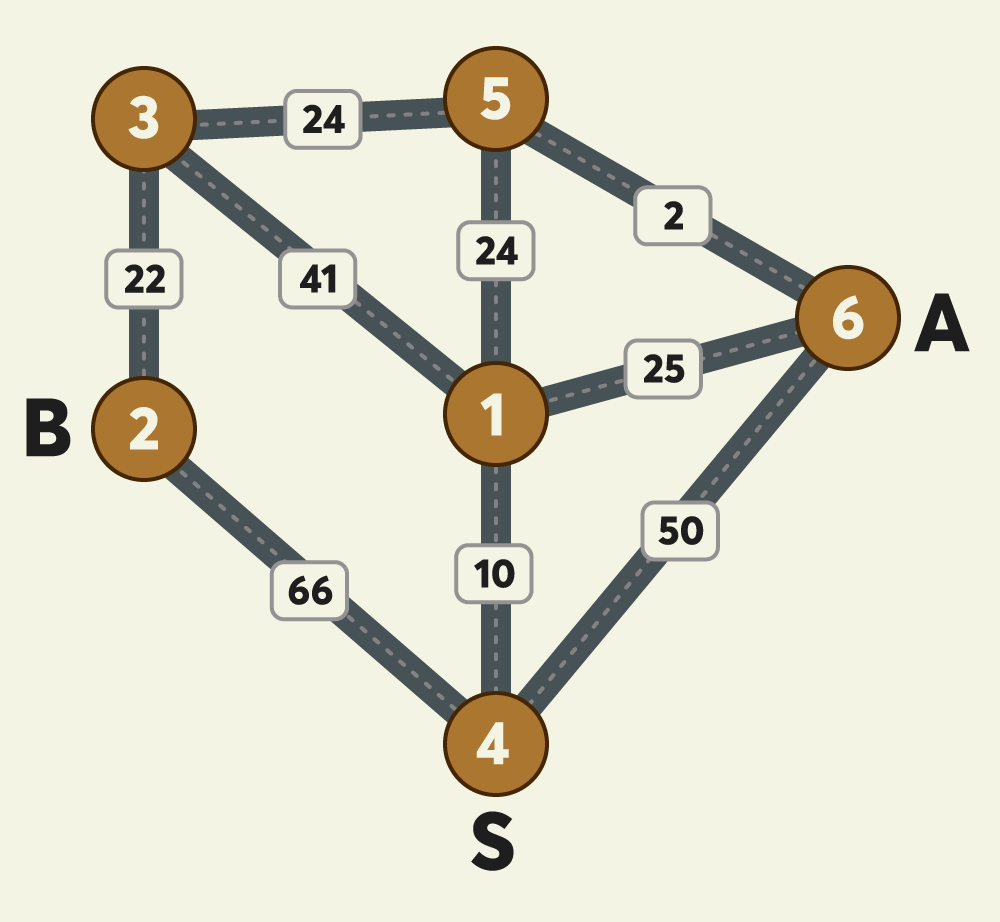
이 문제는 두가지 방식으로 풀이할수있는데, 플로이드워셜이 직관적으로 잘 와닿아서 먼저 소개하겠다.
그리고 다익스트라 알고리즘으로 풀이를 살펴보겠다.
플로이드 워셜 알고리즘 : 최단경로 업데이트하면서 진행
모든 노드에서 다른 모든 노드까지의 최단 경로
다익스트라와 마찬가지로 단계별로 거쳐 가는 노드를 기준으로 알고리즘 수행
- 다만 매 단계마다 방문하지 않은 노드 중에 최단 거리를 갖는 노드를 찾는 과정 필요x ->다익스트라와 차이점
2차원 테이블에 최단 거리 정보 저장
DP에 속함 (2차원 테이블의 값을 점화식에 따라 처리하므로 dp임)
각 단계마다 특정 노드 K 거쳐 가는 경우 확인 - A -> B로 가는 최단 거리보다 A에서 K를 거쳐 B로 가는 거리가 더 짧은지
- Dab = min(Dab, Dak+ Dkb)
따라서...
=> node[i][j]보다 node[i][k] + node[k][j] (k를 경유해서 가는 방법)이 더 작은 값이라면 갱신해준다.
이런 방법으로 모든 노드에서 모든 노드로 가는 최단 경로를 알 수 있다. 시간 복잡도는 O(n^3)으로 다소 오래걸리는 편이다.
import java.util.Arrays;
//플로이드 워셜
class Solution {
static final int MAX = 20000001; // 200 * 100000 + 1
public int solution(int n, int s, int a, int b, int[][] fares) {
int[][] dp = new int[n + 1][n + 1];
for (int i = 0; i <= n; i++) {
Arrays.fill(dp[i], MAX);
dp[i][i] = 0;
}
for(int i = 0; i < fares.length; i++) {
int start = fares[i][0];
int end = fares[i][1];
int cost = fares[i][2];
dp[start][end] = cost;
dp[end][start] = cost;
}
//플로이드워셜 알고리즘으로 최단경로 cost 업데이트
for(int k = 1; k < n+1; k++) {
for(int i = 1; i < n+1; i++) {
for(int j = 1; j < n+1; j++) {
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);
}
}
}
int answer = dp[s][a] + dp[s][b];
// 경유지점을 끼는경우
// s -> t t -> a + t -> b
for(int i = 1; i <= n; i++) {
answer = Math.min(answer, dp[s][i] + dp[i][a] +dp[i][b]);
}
return answer;
}
}
다익스트라 알고리즘 : 개선된 다익스트라 =>우선순위 큐
우선순위 가장 높은 데이터 가장 먼저 삭제하는 자료구조
- 그리디 알고리즘 : 매상황에서 방문하지 않은 가장 비용이 적은 노드 선택
- 단계 거치며 한번 처리된 노드(이미 방문 처리)의 최단 거리는 고정되어 바뀌지 않음
- 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해
- 다익스트라 수행 후 , 테이블에 각 노드까지의 최단 거리 정보가 저장됨
- 단계마다 방문하지 않은 노드 중 최단 거리 가장 짧은 노드 선택하기 위해 매 단계마다 1차원 테이블의 모든 원소를 확인(순차 탐색)
S에서 모든 위치의 최소 거리
A에서 모든 위치의 최소 거리
B에서 모든 위치의 최소 거리 만 구하면 됨.
import java.util.*;
class Edge implements Comparable<Edge>{
int index;
int cost;
Edge(int index, int cost){
this.index = index;
this.cost = cost;
}
@Override
public int compareTo(Edge e){
return this.cost - e.cost;
}
}
class Solution {
static final int MAX = 20000001; // 200 * 100000 + 1
static ArrayList<ArrayList<Edge>> graph;
public int solution(int n, int s, int a, int b, int[][] fares) {
int answer = Integer.MAX_VALUE;
graph = new ArrayList<>();
for(int i = 0 ; i <= n ; i ++){
graph.add(new ArrayList<>());
}
for(int[] i : fares){
graph.get(i[0]).add(new Edge(i[1], i[2]));
graph.get(i[1]).add(new Edge(i[0], i[2]));
}
int[] startA = new int[n + 1];
int[] startB = new int[n + 1];
int[] start = new int[n + 1];
Arrays.fill(startA, MAX);
Arrays.fill(startB, MAX);
Arrays.fill(start, MAX);
//S,A,B에서 모든 위치의 최소거리를 구함
startA = dijkstra(a, startA);
startB = dijkstra(b, startB);
start = dijkstra(s, start);
//for문으로 1~n까지 i번째부터 따로 가는방식으로 계산한 거리 중 최소값을 정답으로 함.
for(int i = 1; i <= n ; i ++) answer = Math.min(answer, startA[i] + startB[i] + start[i]);
return answer;
}
static int[] dijkstra (int start, int[] costs) {
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(start, 0));
costs[start] = 0;
while (!pq.isEmpty()) {
Edge now = pq.poll();
int nIndex = now.index;
int nCost = now.cost;
if(nCost > costs[nIndex]) continue;
ArrayList<Edge> edges = graph.get(nIndex);
for (Edge edge : edges) {
int cost = costs[nIndex] + edge.cost;
if (cost < costs[edge.index]) {
costs[edge.index] = cost;
pq.offer(new Edge(edge.index, cost));
}
}
}
return costs;
}
}
카카오에서 플로이드워셜 문제를 몇차례 본 것 같다. 전체적인 흐름에 대한 파악을 통해 플로이드 워셜을 사용하는 방식을 익혀두어야 될 필요성을 느꼈다.
반응형
'코딩테스트 > Java' 카테고리의 다른 글
| [JAVA] 백준 어른상어 (0) | 2021.10.05 |
|---|---|
| [JAVA] 백준 경사로 (0) | 2021.09.28 |
| [JAVA] 백준 마법사 상어와 비바라기 (0) | 2021.09.23 |
| [JAVA] 백준 사다리 조작 (0) | 2021.09.16 |
| (2021 카카오) 광고삽입 JAVA (0) | 2021.09.11 |